Tipográfia a matematikaórán

Egy példa arra, hogyan szerettessük meg a matematikát

Hosszú éveken át szerveztem matematikatáborokat az iskolámban. Nem kezdtük korán a foglalkozásokat, hiszen előző este általában sokáig fent voltunk, társasoztunk, beszélgettünk. Diákjaink nem voltak speciálismatematika-tagozatos gimnazisták, így kollégáimmal együtt úgy éreztük, hogy egy téma felvetése, tárgyalása, majd néhány elmélyítő feladat elegendő a matematikát kedvelő fiatalok számára. Ebéd után valami mást kellett csinálni. Általában elmentünk kirándulni, csak vacsorára jöttünk vissza. Megelőzendő azt a szokásos kérdést, hogy „Sok van még?” vagy „Mikor érünk már oda?”, fejtörőkkel készültünk az útra. Sokszor a fejtörők olyan jól sikerültek, hogy az egész út alatt lekötötték a diákok figyelmét, és a vacsora után is vissza kellett térni rájuk. A korábbi kérdéseket felváltották a logikai feladványokkal kapcsolatos érdeklődések, megoldásvázlatok. Szép emlékek ezek a túrák.

A bevezetőben említett kedves „elterelő hadművelet” késztetett arra, hogy a hosszú távolléti tanítást érdekessé tegyem, s a számítógép mögött is különlegessé tehessem az órát a gyerekek számára.

1. Iskolai háttér

Mindannyiunkat nagyon váratlanul ért a pandémia miatti iskolabezárás, illetve az az igény, hogy az interneten keresztül kell tanítanunk. Ugyan már egy ideje láttuk, hogy nem tehetünk mást a járvány megfékezése érdekében, de a megvalósításról nem sok tapasztalatunk volt. Magam is gondokkal tele kezdtem neki az első ilyen „online órának”, jóllehet már szeptember óta így tartottam a módszertanos óráimat az ELTE-n a hallgatóknak.

Nagy szerencsém van az iskolámmal, hiszen a felkészülésre az igazgatónk lehetővé tett számunkra néhány napot értekezletekkel, megbeszélésekkel. Azon túl, hogy felmértük az igényeket (s ha kellett, kaptunk iskolai segítséget otthonunk „gépesítésére”), kisebb csoportokban (néha tanítási szakok szerint, néha éppen vegyesen válogatva, hogy további ötleteket „lophassunk” egymástól), megbeszéltük az óratartás új kérdéseit: hiányzások, táblahasználat, ellenőrzés, számonkérés stb. A további felkészülést, a különböző platformok, lehetőségek használatát egy-egy, a technikában járatosabb kolléga segítségével sajátítottuk el.

Szerencsénk van abban a tekintetben is, hogy diákjainknak otthon általában volt számítógépük és internetelérési lehetőségük, és sok esetben a családtagok el tudtak különülni egymástól, hogy ne zavarják egymást a munkában. Az iskola alapítványai tudták támogatni a diákokat anyagilag, számítógéppel, valamint a szülői felajánlások is lehetővé tették, hogy mindenki nagyjából ugyanolyan erőforrásokkal rendelkezzen a hosszú otthonlét alatt.

Nem szabad arról sem megfeledkezni, hogy iskolánk diákjai igen motiváltak a tanulásban, valamint a közös munkában. Az általunk sokat emlegetett „Eötvös-szellem” nagyban támogatta a munkánkat, hiszen a diákok sok tekintetben építhettek egymás segítségére is.

2. A LaTeX szövegszedő rendszer használata

A műszaki tanulmányokat végzők számára nem ismeretlen a TEX program. Azoknak, akik még nem találkoztak ezzel a szövegszedő programmal, néhány mondatban szeretném bemutatni, mivel ezzel támogatva valósítottam meg a diákokkal közösen a matematikaóráinkat.

Egy kis történelem

Egyetemi éveim alatt komoly kihívást jelentett a szakdolgozat begépelése, hiszen addigra már szinte elvárás volt (különösen informatika szakos hallgatók számára), hogy a hagyományos írógéppel készült forma helyett számítógépes szövegszerkesztővel hozzuk létre művünket. Akkor még igencsak gyerekcipőben járt a Windows Word nevű szövegszerkesztője, s nehézkes volt pl. a sok fizikaképlet beírása. Az sem sokat segített, hogy a Word helyett szívesen használtam az OS/2 operációs rendszer szövegszerkesztőjét, hiszen ebben a programban is nehézkes volt a képletek begépelése, s a nagyobb, több oldalas írásokkal nehezen boldogult a kevéske memóriával rendelkező gépünk.

Ebben a „történelmi múltban” ismertem meg Donald Knuth matematikus (1978 óta folyamatosan fejlesztett) TEX szövegszedő programját, ami kis eszközigénye, valamint a parancsok egyszerűsége miatt megváltás volt számunkra. Igaz, nem volt a megszokott wysiwyg környezet (what you see is what you get – azt kapod, amit látsz), s csak a program lefuttatása (fordítás) után láttuk, hogyan is néz ki a papíron a kész szöveg, mégis lenyűgözött minket könnyű használata és tipográfiailag kifogástalan „kimenete”.

A program hátterében Knuth zseniális programozói tehetsége áll. A szöveget a szerkesztő parancsokkal együtt egy egyszerű editor használatával visszük be, s a parancsként megadott formátumban fordítás után (.dvi, .ps, vagy akár .pdf állományban) kapjuk vissza. Az egyes parancsok (helykihagyás, igazítás, betű formátuma, matematikai képletek parancsai...) azon szövegrészek mellett találhatók, amelyekre vonatkoznak, így könnyű átlátni azt, hogy mit is szerkesztettünk a dokumentumunkon. Emellett szemet gyönyörködtető az új betűtípus (cmr – computer modern roman), aminek leírásához szintén matematikai függvények segítenek a háttérben. Nekünk, matematika-fizika szakos tanároknak a jól átlátható, nyomdász szemmel hibátlan képletek teszik igazán széppé, kedvessé a programot.

Talán feltűnő volt eddigi szóhasználatomban, hogy az említett programra nem a szövegszerkesztő, hanem a nyomdászatban használatos szövegszedő szót használom. Valóban, a TEX azt a munkát modellezi számítógépes program segítségével, ahogyan a nyomdász eligazgatja a betűsínben a betűket, ha kell, akkor kiegyenlíti a szavak közötti űrt, hogy a sorok végei egymás alá kerüljenek, a kész sorokat pedig úgy illeszti egymáshoz, hogy azok az oldalon szépen mutassanak.

Ugyan a TEX felhasználói ismerete nem igényel túl sok tanulást (néhány parancs magtanulása után könnyen használhatjuk már a programot), mégis nehéz azt jól használni, hiszen kevesen rendelkezünk alapvető nyomdászati ismeretekkel. (Más szövegszerkesztőkkel készült dokumentumok is igen árulkodnak erről a hiányosságunkról...) Ezt segítendő hozta létre Leslie Lamport azt a L^ATEX-nek hívott programrendszert, mely a TEX parancsait kisebb csomagok segítségével teszi könnyen használhatóvá. Így pl. megadhatjuk a készülő dokumentumunk típusát (levél, cikk, könyv stb.), és e csomag beállítása után a program (a megfelelő formázási parancsokkal) automatikusan készíti el a kívánt formátumú írást, s nem kell a cím, alcím, dátum... elhelyezésével bajlódnunk. Természetesen tudunk változtatni a formázáson, ha vagyunk olyan bátrak, hogy a nyomdászatilag tökéletestől eltérjünk (de ezt csak haladóknak ajánljuk). Emellett a L^ATEX (vagy egyszerűbben LaTeX) lehetővé teszi számos (és egyre bővülő számú) csomag betöltését, így könnyen írhatunk sakkról (kész figurák állnak rendelkezésünkre), kottázhatunk (a komoly kottagrafikusi munkát néhány paranccsal kiválthatjuk), vagy (néhány parancs megismerése után) egyszerűen gépelhetünk kémiai képleteket. Az egyes grafikai csomagok egyszerűvé teszik a táblázatok, képek stb. beillesztését.

(Az érdeklődők részletesen megismerkedhetnek a L^ATEX-hel az Érintőben 2017–18-ban megjelent Miért éppen LaTex? és Latex még egyszer cikkekből. A szerk.)

Azoknak, akik még sosem próbálták, hadd mutassak két példát a forráskóddal együtt.

Az első próbálkozások

Mint említettem, az iskolavezetés az iskolai alapítványok segítségével „minden jóval” felszerelt bennünket az online tanítás támogatására. Így pl. kifejezetten hasznosnak bizonyult az elektronikus palatábla (digitalizáló rajztábla), amellyel a kisebb ábrákat, magyarázatokat meg tudtuk valósítani. (Megjegyzem, a dolgozatok javításánál is igen jól lehetett használni ezt az eszközt.) A hagyományos óratartás innentől valamennyire megvalósulhatott, hiszen a diákok a kérdésekre válaszolva diktálhatták, mi kerüljön a táblára. Ezzel a jegyzeteléshez mintát adhattam, s egyfajta kezdetleges interaktivitás is megvalósulhatott.

Korábbi ismereteim és a viszonylag gyors, tízujjas gépelésem lehetővé tették azt is, hogy a tanulók diktálása alapján a szöveget és a képleteket L^ATEX-parancsként begépeljem, s az egyes diákat (a L^ATEX beamer csomagjának segítségével) a velük megosztott képernyőmre kivetíthessem. A jegyzet ettől fogva szebb lett, de a tanulói aktivitás nem sokat változott. A sok előkészítés (pl. a fizikához az ábrák megrajzolása), a feladatsorok begépelése, stb. még mindig nem hozta meg a kívánt eredményt, az igazi tanulói aktivitást. Természetesen folyamatosan beszélgethettünk, miközben a jegyzetet készítettem, de azt szerettem volna elérni, hogy a jegyzetet a diákok maguk írják, s nem arról szólna az óra, hogy a saját füzetükbe másolják a „táblát”. A fájl elküldése ugyan megoldhatta azt, hogy ne kelljen jegyzetelniük az órán, de azt szerettem volna, ha a viszonylagos passzív szerepből aktív részesei lennének az órának.

Ekkor jutott eszembe, hogy az egyetemen a hallgatók sok esetben megosztják velem a készülő szakdolgozatukat egy, az interneten működő virtuális számítógépen futó L^ATEX program segítségével, s így én is bele tudok írni egy-két megjegyzést a készülő dolgozatba. Az új felületet (néhány éve használható az overleaf.com felületen a L^ATEX) korábban még nem használtam úgy, hogy egyszerre 15-20 ember is szerkesztené azt...

3. Az órák gyakorlati megvalósítása

Az overleaf.com felületen található L^ATEX program várakozáson felül jól működik. Általánosságban igaz, hogy a 10–15 felhasználó (akik aktívan szerkesztik) nem jelent gondot. Esetenként a túl sok grafikon – komoly, számításigényes pl. tikzpicture-ábrák, rekurzív-képletek (pl. fraktálok készítése a lindenmayer csomaggal) – lassította a program futását, vagy a fordítóprogram jelzett memóriahiányt. (Ezek a fizetős változattal elkerülhetők.) A gyerekek hamar észrevették, hogy a hasonlóképpen megosztható google-dokumentumok többségével ellentétben, ebben a programban nagyon könnyen szerkeszthetjük pl. a képleteinket, és gyönyörű .pdf kimenetet kapunk, amelyet (a forráskóddal együtt (.tex állomány)) könnyen letölthetünk.

Bevallom, az első órára készülve aggódtam, hogy a diákok számára érdekes lesz-e a program használata, s nem veszi-e el a kedvüket a néhány parancs megtanulása. (Ehhez előre elkészítettem egy sablont, ami néhány beállítást tartalmazott (preambulum), s igen koncentráltan csak a legszükségesebb parancsokat mondtam el – természetesen sok személyes, illetve történeti vonatkozás megemlítésével.) Magam is meglepődtem, hogy az óra második harmadában már mindenki képletet szerkesztett, s örömmel nyugtázták, hogy milyen gyönyörű is annak a .pdf állományban megjelent képe. A 45 perces óra végére mindenki önállóan tudott dolgozni, sőt már egymást javították, segítették a munkában.

Az „élő” tanítási óra hangulatát adta vissza az is, hogy a tanulópárok (egész évre van a csoportokban ilyen beosztás, akik egymást segítik az órán és délután a tanulásban) elkezdtek egymással kommunikálni akár a háttérben, akár csak úgy, mindenki füle hallatára. Ettől a pillanattól fogva éreztem, hogy megtaláltam a jó munkaformát.

A diákok hol párban (tanulópárok), hol nagyobb csoportokban egymást támogatva dolgoztak. A mindennapi életben megfigyelhető ez a munkaforma (a team-munka): közös ötletelés, majd az egyik fél írja a konkrét feladatot, míg a másik segít, ellenőriz, építő jelleggel kritizál, utána cserélnek. Számomra is egészen más típusú feladatot jelentett az óratartás: délutánonként előre kitalált feladatokat gépeltem be, tettem közzé a következő órához, vagy ellenőriztem a – szintén ebben a dokumentumban található – házi feladatokat. Az órán szemet gyönyörködtető volt látni a 15–16 fő aktív munkáját, hallgatni a párbeszédeiket. Egy-egy kérdés mind a tanulók részéről, mind felőlem felhívta mindenkinek a figyelmét az esetleges gondokra, diszkusszióra. A kérdésekre örömmel válaszoltak, ha kellett, hamar érkezett a segítség. Az egymáshoz hasonló feladatokat viszonylag könnyű volt áttekinteni, s folyamatosan figyelni a párok haladását. Egy-egy órán így kb. 3–4-szer annyi feladatot tudtunk kidolgozni, mint a hagyományos frontális oktatás során. A hagyományos páros munkaformához képest pedig lényeges különbség volt, hogy a tanulók délutáni készüléséhez minden kidolgozott feladat rendelkezésre állt, hiszen egy közös „füzetbe” készültek a munkák. (Ezeket bárki bármikor lementhette magának.)

Délutáni „leskelődésem” során (hogyan halad a házi feladatok elkészítése, van-e probléma) észrevettem, hogy igen sok esetben továbbra is egymást segítik a tanulók, de immár nemcsak a tanulópárok, hanem 4–5 fős nagyobb csoportok. Természetesen egyrészt az a kényszer, hogy nem lehetett sehová sem elmenni, érthetővé tette ezt a hozzáállást, másrészt nem gondolhatok másra – ezt a későbbi, évvégi értékelésnél a tanulók is megfogalmazták –, mint hogy igen érdekesnek tartották magának a L^ATEX programnak a használatát.

Többféle csoportom is volt, s mindegyikben kipróbáltam ilyen típusú órák megtartását.

A hetedikes csoportban nagyon ügyesen elsajátították a program használatát, s kifejezetten jót tett a jól strukturált írásmód megtanításánál. Így a szöveges feladatokhoz készített táblázatok jól áttekinthetőek lettek, s azokból az egyenletet felírni már gyerekjáték volt. De az egyenletek, egyenletrendszerek megoldásánál is igen tetszetős képet kaptunk néhány szükséges parancs megismerése után. Ezt követően a diákok kifejezetten élvezték azt, hogy egy programcsomag (tikzpicture) megismerésével mennyire egyszerűen készíthetünk grafikonokat, függvényeket. A digitális kultúra c. órán is nagy sikert aratott az, hogy a programozási ismeretek egy részét a L^ATEX program segítségével szereztük meg (pl. do-while-ciklus). Örömmel írtak például olyan programot, ami az első néhány ezer héttel osztható számot nyomtatja ki egy négysoros program eredményeképpen.

A nagyobbaknál (11. és 12. évfolyamosoknál) hamarabb jött meg a sikerélmény, annak ellenére, hogy kezdetben jóval összetettebb parancsokkal kellett megismerkedniük. A komoly grafikonok, ábrák készítése viszonylag nehézkes a kezdő felhasználó számára. Ezt a problémát eleinte úgy léptük át, hogy a jól ismert GeoGebra program L^ATEX-kimenetét illesztettük be a megadott helyre. (Sőt, kezdetben olyan is volt, hogy a GeoGebra programban elkészített képet mint .png, vagy .pdf dokumentumot) helyeztük el a kívánt részre. Az így készült ábrákat később még szebbek váltották fel, amint a komolyabb grafikai csomagokat elkezdtük használni.

Egy-egy komoly ábra megtervezése és kivitelezése nagyobb erőfeszítést igényelt a diákoktól, de ezt ők kihívásnak tekintették, s nem nyugodtak bele a hozzávetőlegesen jól sikerült ábrákba, a tökéletességre törekedtek. Így pl. a sorozatok határértékénél gyönyörűen berajzolták az 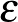$\varepsilon$ -hoz tartozó 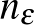$n_\varepsilon$ küszöbindexet. Érdekes volt megfigyelnem, hogy míg a korábbi években megszoktam, hogy ezeket a fogalmakat minden órán újra át- és átbeszélem, újra újabb ábrákat készítve minden órán segítem az elmélyítést, most erre egyáltalán nem volt szükség. A tanulók igen nagy szellemi erőfeszítéssel tervezték s rajzolták be ezeket az értékeket, miközben eltörpült az a probléma, hogy mi is lenne az a küszöbindex. Mint ahogy a kiránduláson a logikai feladványokon töprengve elfelejtették azt, hogy milyen hosszú és fárasztó is a hegyre felmenni, most a konvergencia fogalma szinte magától érthetővé vált (pedig ez a matematikában igen sok beszélgetés, gyakorlás árán szokott megvalósulni). Ezt a jelenséget később több helyen is megfigyeltem. A L^ATEX mint „görcsoldó” gyógyszer segített a matematikai nehézségeken átlépni, az alkotás öröme, a gyönyörű esztétikai eredmény minden tanuló figyelmét elterelte.

A könnyebb elképzeléshez álljon itt egy példa.

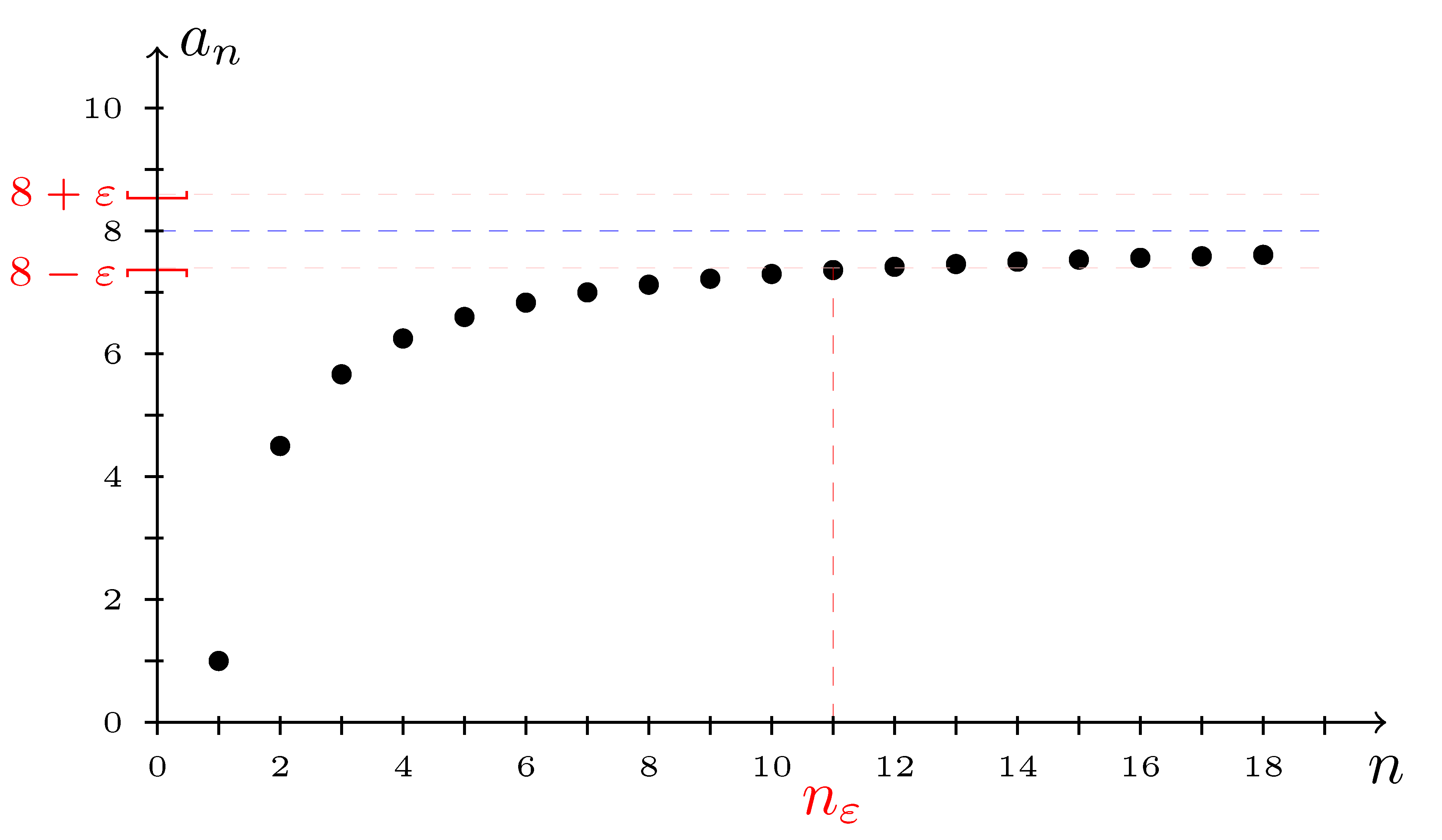
Sok esetben azt figyeltem meg, hogy az addig gyengébben teljesítő diákok örömüket lelik ebben az alkotásban, sikerült oldani a félelmüket a matematikai sikertelenségtől. De azt is észrevettem, hogy egyesek kifejezetten örömüket lelik abban, hogy tovább kutatják a L^ATEX előnyeit, sőt, feszegetik a határokat. Lehetett feszegetni, lehetett próbálkozni, nem volt határ. Külön élmény volt számomra, hogy a végzős osztály két matematikafakultációs tanulóját annyira magával ragadta a – kitekintésként megemlített – fraktálos foglalkozás, hogy maguk utánaolvasva a témának, saját anyagot hoztak létre kezdetben az osztálynak, majd később nagyobb közönségnek is egy komoly KöMaL-cikkben. Közös, majd' féléves projektünk eredménye nem csak a saját felfedezéseik publikálása volt, de egy másik, 10 oldalas cikkben a fraktálos ábrák rekurzív programozásának közlése, bemutatása is elkészült. Mint matematikaszakos tanár, ezt igen komoly munkának könyveltem el.

Íme egy ábra a tanulók által készített rekurzív programozás eredményéről.

Az egyetemi hallgatók néhány órájánál (Elemi matematika 1–4. c. tantárgyak) is felajánlottam ennek a munkaformának a kipróbálását. A későbbi beszámolók alapján is elmondhatom, hogy számukra is nagyon hasznos foglakozások voltak ezek, hiszen hamarosan ennek segítségével írhatják meg a beadandó feladatokat, vagy akár a szakdolgozatukat. (A hallgatók körében komoly kihívás szokott lenni, ha önállóan kell megismerkedniük a program használatával.)

4. Mit kaptak a diákok az órán?

Közel egy év távolléti oktatás után volt alkalmam találkozni pár hétre a diákokkal. Nagyon kíváncsi voltam, hogyan élték meg ezt a fajta tanítást, hogyan érzik, mennyiben volt más a többi órához (korábbi óráimhoz, illetve más tantárgyak tanóráihoz) viszonyítva. Nem csak ebben a pár hétben találkozhattam a diákokkal, a nyári táborok alatt is kötetlenül beszélgethettem velük. (Osztálytábor, tanulmányi tábor, kerékpártábor stb. – idén, az igények miatt, halmozottan sok tábor volt a nyáron.) Közösen összeszedtük, hogy miben volt más ez a munkaforma, s ők miben látják előnyét, hátrányát.

Kezdem a gondokkal. Ahogy én is, a diákok is félve álltak az ötletem előtt, nem gondolták, hogy könnyen fog menni a (többé-kevésbé) tízujjas gépelés elsajátítása, a parancsok megértése, használata. Úgy érezték, hogy a matematika tantárgyban az órai személyes találkozások elengedhetetlenek a jó megértéshez. Ezeket a problémákat valójában, véleményük szerint is, csak az ismeretlentől való félelem szülte, kiderült, hogy sokkal többet tudnak velem és egymással is dolgozni ebben az új környezetben. Igen hasznosnak vélték a közös jegyzetet, ami jóval több gyakorlatot tartalmazott, mint az eddigi füzeteik. (Persze, most is voltak olyanok, akik délutánonként átmásolták a számukra lényegesnek tartott dolgokat a füzetükbe.)

A tanulók kifejezetten érdekesnek tartották azt, amikor elmeséltem, hogy hány munkahelyen dolgoznak hasonló módszerekkel a szüleik. Többen otthoni rákérdezés után megerősítették ezt az állításomat.

A diákok külön kiemelték, hogy az ismerős környezet már a második héten megnyugtatta őket, pontosan tudták, hogy mit várjanak ezektől a matematikaóráktól. A tanórák gördülékeny lefolyását, az „idő elrepülését” is többen említették. A strukturált írásmód, a jól áttekinthető jegyzet (dátumozás, tartalomjegyzék...) szintén említésre került. Többen szeretnék valamilyen módon a jegyzeteket folytatni, örülnének, ha saját magunk által írt könyvből, jegyzetből tanulhatnának. (A tanév alatt arra is volt példa, hogy néhány diák a témazáró dolgozat előtt egy saját összefoglalást készített az anyagról, amit ellenőrzésre, áttekintésre én is megkaptam.)

Az utolsó hetekben a saját osztályomban előkerült a nyomdászat, a tipográfiai ismeretek témája. Ennek kapcsán beszélgettünk magáról a gutenbergi könyv jelentőségéről, valamint a könyvkötésről. Az elmélet rövid áttekintése kapcsán rávettek, hogy a saját balatoni nyaralásunk során tanuljunk meg könyvet kötni. Igen büszkék voltunk az egyhetes tábor alatt elkészült gyönyörű művekre. (Igen nagy logisztikai szervezést jelentett, hogy a táborra ekkora létszámra minden felszerelést előteremtsek. A cél érdekében a papír, a szürke lemez, a vászon, ragasztóanyagokon keresztül a vágó- és présgépig mindent le kellett vinni. Hallatlan élmény volt tanítgatni őket.)

A diákok nem nagyon vették észre, de saját tapasztalatom alapján kifejezetten figyeltem arra, hogy a gépelés közben ejtett hibákat milyen hatékonysággal találják meg a sorok között. A nagy fejlődés mindenkinél megfigyelhető volt. Ez külön öröm volt számomra, hiszen évek óta sok fogadóórán kérdezik a szülők, hogy mivel lehetne a gyerekek pontosságát fejleszteni, figyelmüket növelni. Erre korábban mindig valamiféle társasjátékot javasoltam, amelynél a hibázás büntetést von maga után, de ennek talán nem olyan nagy a tétje, mint a matematikadolgozatban keletkezett figyelmetlenségből adódó hibáké. A gyors hibakeresés fokozta az odafigyelést, a precizitást, s ez biztosan a jövőben is meg fog térülni a matematikai feladatok megoldásánál .

Összefoglalva, úgy látom, hogy a rengeteg szakmai (matematikai, informatikai, tipográfiai) ismeret mellett számtalan kedvező hozadéka volt ennek a tanítási munkaformának. A nyár alatt szeretnék tervet kidolgozni arra, hogy milyen módon lehetne élni evvel a lehetőséggel akkor is, amikor ismét az osztályteremben tudunk dolgozni.